第一次作业:
个人思路: 1.输入 2.对输入进行基本的判断 (1)通过string.split(),将每个数分割出来 //在此步遇到的困难是,以+/-去分割时,要排除掉++连续的清空,把例如++19x^+2,分割出+19x^+2。 在分割上,无非对应以下几种分割 1.常数 +19 2.x +x 3.x^n +x^n 4.+ +ax^+n//这之中还有空格的干扰 (2)对分割出来的每个数进行判定,判断是否符合格式 3.将分割出的项进行处理 (1)项中的空格处理 4.对每个项进行求导 (1)套用求导公式 (2)注意数字允许带前导0 (3)注意常数项 (4)注意x^0,求导视为常数项 (5)注意系数为+1/-1时,可以省略1进行输入 5.对求导完毕之后的项进行对应输出 然后开始debug 测试点问题:1+1 输出无 正确输出0 原因:在输出时忽略了判断条件到底什么时候去输出0 测试点问题:2x^3+2x^4 输出:6x^28*x^3 原因忽略了符号的加入 测试点问题:1+ 输出:0 正确输出:WRONG FORMAT! 原因:在分割之后只是去判断了1,而忽略了对+的判断 位图:
复杂度:
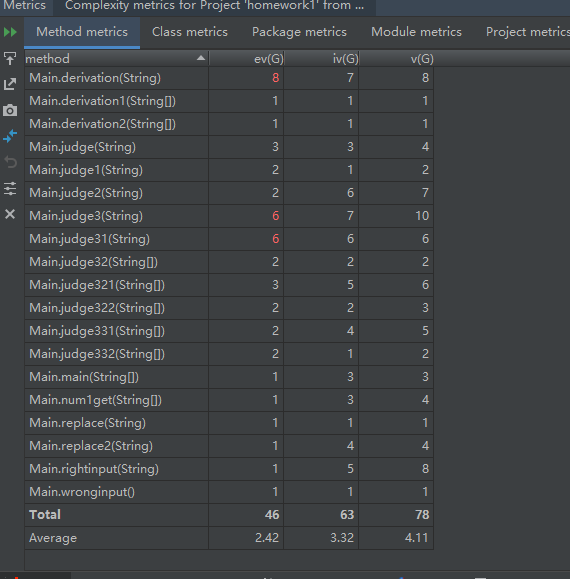
总结:在第一次作业中,对于面向对象的操作并不是很熟悉,所以大概率还是采用了面向过程的编程方式。
第二次作业:
与第一次作业的差别:增加了sin(x)、cos(x)以及所对应的指数形式,如sin(x)^+2 易错点:sin与cos中不能出现空格,即s i n不符合情况,与先前的常数项中不能有空格相同 个人思路: (Ⅰ)wronginput部分 1.匹配是否出现了其他非法字符,利用将合法字符全部删除来检测是否有其他字符方法来实现。 主要调用函数:string.replaceAll(); 2.以+号为分割,将各个部分分开,称之为项1. /这一部分有可能出现++|+-|-|--的形式,利用++为+,+-不变,-+为+-,--为+的方式进行屏蔽化简 与此同时,对于指数上出现正号的情况,利用正则表达式将其屏蔽化简,如x^+6,对应正则表达式为x\s\^\s\+\s\d去进行化简/ 3.对于各个风格的部分,利用正则表达式去进行匹配,不合法的部分wrong输出 /以一个包含了各个方面的正确例子为制造正则表达式 2sin(x)^+2 7x+7x8x+3sin(x)cos(x)xsinx^+3/ 4.由于在上一步进行分析的时候发现,可能会出现(中强测一定会出现)多元因子连乘的情况,所以我准备再用号对项1进行分割,从而得到项二,对于项二利用正则表达式进行匹配,对于不合法的项wrong输出。 /先利用trim将项2的前后空格去掉,这样在匹配过程中就会减少对于\s的匹配,从而提升利用率 项2的合法正则表达式: [+-]?[(sin)(cos)]?\s\(x\)(\s\^\s\d)? || [+-]?\s\d\s/ (Ⅱ)rightinput部分 1.经过wronginput检测后,可以确定所有空格对本表达式均无害,所以将全部空格去掉化简 /主要调用函数:string.replaceAll("\s","');/ 2.将整个表达式进行符号的化简,依旧采用+号进行分割的方式,我们将分出的项称为项1,同wrongingput中的第二步相同 /这一部分有可能出现++|+-|-|--的形式,利用++为+,+-不变,-+为+-,--为+的方式进行屏蔽化简 与此同时,对于指数上出现正号的情况,利用正则表达式将其屏蔽化简,如x^+6,对应正则表达式为x\s\^\s\+\s\d去进行化简/ 3.将项1中的式子进行乘法化简 /具体化简有:以号去划分项1中的每一项得到项2,继而将项2中相同性质的项进行乘法运算,如 这里有个小坑就是-sin(x)应该先做一个分解,将其变为-1sin(x),+同上 \d\d得到常数1 x^\d x^\d 得到x项 sin(x)\^\d * sin(x)\^\d 得到sin项 cos(x)\^\d * cos(x)\^\d 得到cos项 化简到最后的情况会变为(\d\)?(x\^(-)?\d\)?(sin\(x\)\^(-)?\d\)?(cos\(x\)\^(-)?\d\) 即:num1x^num2sin(x)^num3cos(x)^num4/ 4.将化简之后的式子进行求导 /我们将所有整合后的式子全部变为num1x^num2sin(x)^num3cos(x)^num4这样的标准形式 这样再求导的过程中,可以直接利用通式 num1num2x^(num2-1)sin(x)^num3cos(x)^num4+num1num3x^(num2)sin(x)^(num3-1)cos(x)^(num4+1)-num1num4x^(num2)sin(x)^(num3+1)cos(x)^(num4-1) 从而可以得到求导的结果/ 5.将求导后的式子进行化简 通过寻找求导后的式子是否有相同的x、sinx、cosx的指数从而去进行一个同类项的合并 为了使得化简更加的精炼,我们对上一步求导后返回各项的系数,指数,即新的num11,num12,num13,num14,+num12,num22,num32,num42,+num13,num23,num33,num43 共12组数字,并采用空格与+号进行分割 如果num11、num12、num13为0,那么第一组|第二组|第三组不做处理 接着将非零的项用ArrayList存起来 如果num12,num13,num14与后置相同 那么合并同类项进行num11的计算,将原项删除,并且将合并的项动态数组ArrayList存起来 6.输出化简得项 结束程序 wa点:sin(x)^ sin (x) 23+sin(x)+3+x^8 +++x \f1 \v1 +++ + 1+1 x+-1 x*++1 位图:
复杂度:
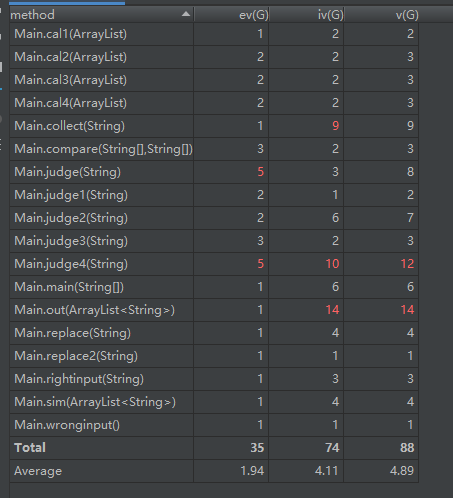
总结:在第二次过程中,自我感觉运用了部分面向对象的知识,但是对于建类的操作不是很熟悉,所以还是只有一个大程序,通过函数来完成自己的目标,这也为后面第三次作业的失败埋下了伏笔。
第三次作业:
个人思路: 这次作业是对上两次作业的升级 在功能性上,引入了复合函数的求导,表达式叠加括号作为因子 举个栗子:sin((sin(x)+cos(x)))^2 注意的是sin(sin(x)+cos(x))^2是错误的,区别于上面 原因在于sin()中是表达式sin(x)+cos(x)所以应该要为(表达式)的形式才可以 那么在这里就出现了一个问题,在上两次作业中,笔者都是采用+号作为分割项,但此次多了表达式作为因子,所以要思考如何将表达式子中的+号进行改变 以sin((sin(x)+cos(x)))^2 + -cos(x^2)为例 笔者在第三次作业中纠结于两个问题 一个是链式法则的构造,一个是复合函数的递归求导 由于第二次作业采用了通式,在第三次作业中不得不对整体作业重构,重构就带来了问题。构造的问题过于复杂,对于类之间的运用一脸迷茫。 复合函数的递归求导直接爆炸,无法判断格式,也求不出导数,因此这里就不放第三次代码图了,实在是惨不忍睹。最后迫于无奈,想着总不能写了那么久不交,虽然最后还是无效作业了,但是也算是努力过了。在之后的过程中继续加强对于面向对象的学习。